跳到主要内容

数据结构 递归是什么？

递归是什么​

递归单纯就是找到解决问题的最小单元，然后不断调用自身

先来理解一下递归

先写一个会导致堆栈溢出的例子：

def countdown(i):
  print i
  countdown(i - 1)

编写递归是必须告诉它何时停止递归。正因此，每个递归都有两个条件：

  1. 基线条件（base case）
  2. 递归条件（recursive）

递归条件指的是函数调用自己，而基线条件是则是指的函数不再调用自己，从而避免无限循环

再来给上面的死循环加上基线条件

def countdown(i):
  print i
  if i <= 1         # 基线条件
    return
  else :            # 递归条件
    countdown(i - 1)

递归如何使用？​

递归的模板，基线条件（终止条件），递归调用，逻辑处理。

public ListNode reverseList(参数0) {
    if (终止条件)
        return;

    从头开始，逻辑处理（可能有，也可能没有，具体问题具体分析）

    //递归调用
    ListNode reverse = reverseList(参数1);

    从尾开始，逻辑处理（可能有，也可能没有，具体问题具体分析）
}

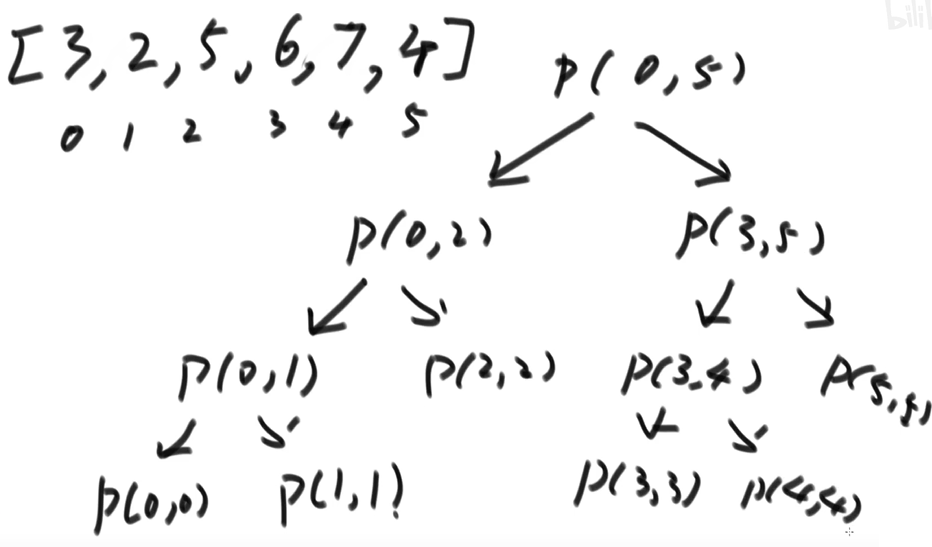
示例：求数组中最大值​

求数组中的最大值

public static int getMax(int[] arr) {
    return process(arr, 0, arr.length - 1);
}

public static int process(int[] arr, int L, int R) {
    // base case
    if (L == R) return arr[L]; // arr[L..R] 范围上只有一个数，直接返回

    int mid = L + ((R - L) >> 1); // 中点
    int leftMax = process(arr, L, mid);
    int rightMax = process(arr, mid + 1, R);

    return Math.max(leftMax, rightMax);
}

执行过程如下：

经典题：反转链表​

输入一个链表，反转链表后，输出新链表的表头。

示例1 输入

{1,2,3}

返回

{3,2,1}

题解

public ListNode ReverseList(ListNode head) {
    //终止条件
    if (head == null || head.next == null) return head;
    // ===============递的阶段===============
    //保存当前节点的下一个结点
    ListNode next = head.next;
    //从当前节点的下一个结点开始递归调用
    ListNode reverse = ReverseList(next); // 这里可以直接取得最后一个 Node
    // ===============归的阶段===============
    // reverse 是反转之后的链表，因为函数 reverseList
    // 表示的是对链表的反转，所以反转完之后 next 肯定
    // 是链表reverse的尾结点，然后我们再把当前节点
    // head挂到next节点的后面就完成了链表的反转。
    next.next = head;

    // 这里head相当于变成了尾结点，尾结点都是为空的，否则会构成环
    head.next = null;
    return reverse;
}

递归和迭代的区别​

参考资料 递归与迭代的区别 参考资料 递归和迭代

在继续学习下面的遍历之前，先来看下迭代和递归的区别，以及下面一节的递归转迭代

递归

递归是有去（递去）有回（归来），因为存在终止条件，比如你打开一扇门还有一扇门，不断打开，最终你会碰到一面墙，然后返回，其过程相当于树的深度优先遍历。

递归的递去和归来：

  1. 递归的递去：原问题必须可以分解成若干个子问题，而且子问题须与原始问题为同样的事（相似），且规模更小
  2. 递归的归来：子问题的演化必须有一个明确的终点，否则可能导致无限递归（无终止条件的循环），也就是说不能无限制地调用本身，须有个出口，化简为非递归状况处理

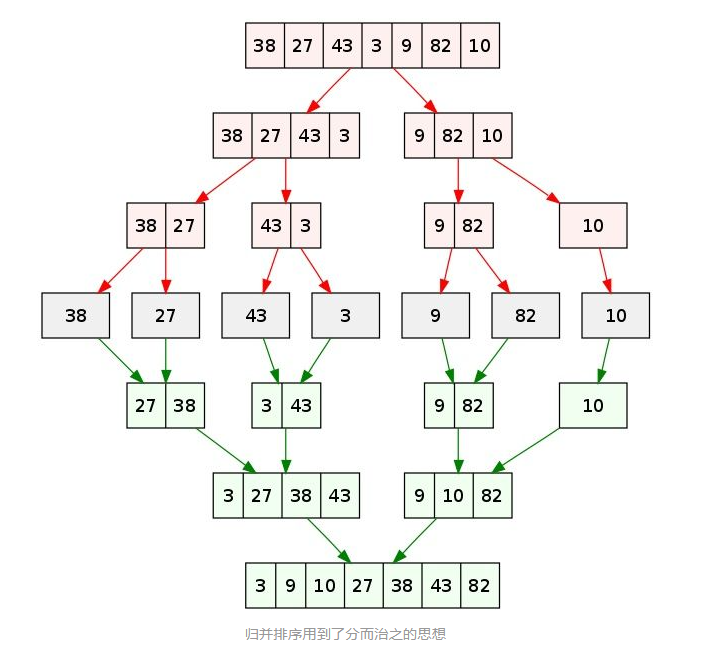
这里再放一张归并排序的图

image.png

迭代

是一个环结构，从初始状态开始，每次迭代都遍历这个环，并更新状态，多次迭代直到到达结束状态。

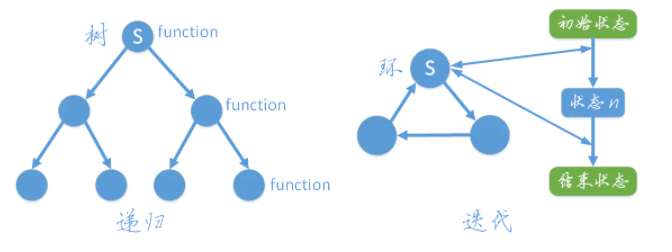
理论上递归和迭代时间复杂度方面是一样的，但实际应用中（函数调用和函数调用堆栈的开销）递归比迭代效率要低。

递归的解题步骤​

转载自 一文学会递归解题

我们在上一节仔细剖析了什么是递归，可以发现递归有以下两个特点

  • 一个问题可以分解成具有相同解决思路的子问题，子子问题，换句话说这些问题都能调用同一个函数
  • 经过层层分解的子问题最后一定是有一个不能再分解的固定值的（即终止条件），如果没有的话，就无穷无尽地分解子问题了，问题显然是无解的。

所以解递归题的关键在于我们首先需要根据以上递归的两个特点判断题目是否可以用递归来解。

经过判断可以用递归后，接下来我们就来看看用递归解题的基本套路（四步曲）：

1、先定义一个函数，明确这个函数的功能（就是定义一个空壳），由于递归的特点是问题和子问题都会调用函数自身，所以这个函数的功能一旦确定了， 之后只要找寻问题与子问题的递归关系即可

2、接下来寻找问题与子问题间的关系（即递推公式），这样由于问题与子问题具有相同解决思路，只要子问题调用步骤 1 定义好的函数，问题即可解决。所谓的关系最好能用一个公式表示出来，比如 f(n)=n∗f(n−)f(n) = n * f(n-) 这样，如果暂时无法得出明确的公式，用伪代码表示也是可以的, 发现递推关系后，要寻找最终不可再分解的子问题的解，即（临界条件），确保子问题不会无限分解下去。由于第一步我们已经定义了这个函数的功能，所以当问题拆分成子问题时，子问题可以调用步骤 1 定义的函数，符合递归的条件（函数里调用自身）

3、将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中

4、最后也是很关键的一步，根据问题与子问题的关系，推导出时间复杂度,如果发现递归时间复杂度不可接受，则需转换思路对其进行改造，看下是否有更靠谱的解法

解题步骤实战演练​

转载自 一文学会递归解题

热身赛​

输入一个正整数 n，输出 n! 的值。其中 n!=123…n，即求阶乘

套用上一节我们说的递归四步解题套路来看看怎么解

1、定义这个函数，明确这个函数的功能，我们知道这个函数的功能是求 n 的阶乘，之后求 n-1, n-2 的阶乘就可以调用此函数了

/**
 * 求 n 的阶乘
 */
public int factorial(int n) {
}

2、找问题与子问题的关系 阶乘的关系比较简单， 我们以 f(n)f(n) 来表示 n 的阶乘， 显然 f(n)=n∗f(n−1)f(n) = n * f(n - 1) ,同时临界条件是 f(1)=1f(1) = 1 ,即

f(n)={1,n=1n∗f(n−1)f(n) = \left\{ \begin{aligned} 1,n = 1 \\ n * f(n-1) \end{aligned} \right.

3、将第二步的递推公式用代码表示出来补充到步骤 1 定义的函数中

/**
 * 求 n 的阶乘
 */
public int factorial(int n) {
    // 第二步的临界条件
    if (n < =1) {
        return1;
    }

    // 第二步的递推公式
    return n * factorial(n-1)
}

4、求时间复杂度 由于 f(n)=n∗f(n−1)=n∗(n−1)∗....∗f(1)f(n) = n * f(n-1) = n * (n-1) * .... * f(1) 总共作了 n 次乘法，所以时间复杂度为 n。

爬楼梯问题​

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

按照上面所说，从最简单的情况开始分析几次，找出反复做的操作。

分析：

a. 如果 1 个台阶，只能从平地上迈上去，所以方式只有 1 种; (1)

b. 如果 2 个台阶，可以从平地上或者第 1 个台阶上上去，所以方式只有 2 种; (1, 1), (2)

c. 如果 3 个台阶，只能从第 1 个台阶或者第 2 个台阶上上去，从平地到第 1 个台阶有 1 种方式是情况 a，从平地到第 2 个台阶有 2 种方式是情况 b，那么， 到第 3 个台阶的方式 = 情况 a + 情况 b

d. 如果 n 个台阶，只能从第 n - 1个台阶或者第 n - 2 个台阶上上去，那么， 第 n 个台阶的方式 = 情况 n-1    + 情况 n - 2

f. 重复操作：stair(n) = stair (n-1) + stair (n - 2)； 只有 1 个或者2 个台阶的情况除外

写递归：

  • 终止条件：根据上面分析当台阶 小于 3 个的时候，不存在以上的重复操作： stair(n) = stair (n-1) + stair (n - 2)

  • 处理逻辑：就是上面的重复操作部分 stair(n) = stair (n-1) + stair (n - 2)

编写代码：

class Solution:
    def climbStairs(self, n: int) -> int:
        if n < 3:
            return n
        return self.climbStairs(n-1) + self.climbStairs(n-2)

递归的时间复杂度​

时间复杂度可以简单的理解成，在某个范围内你做了多少件事，而在上面的代码中，我们做的事只有 2 件，self.climbStairs(n-1) 和 self.climbStairs(n-2)，但是随着递归的深入，我们做的事就变成了

2 x 2 x 2 x 2 x...

此时的时间复杂度为 O(2n)O(2^n) ,因为时间复杂度呈指数型增长，所以当 n 变大时，计算的时间越来越长最后导致超时

这里先看一张图，用来表示上面爬楼梯题目的计算关系 （当 n > 3 时)

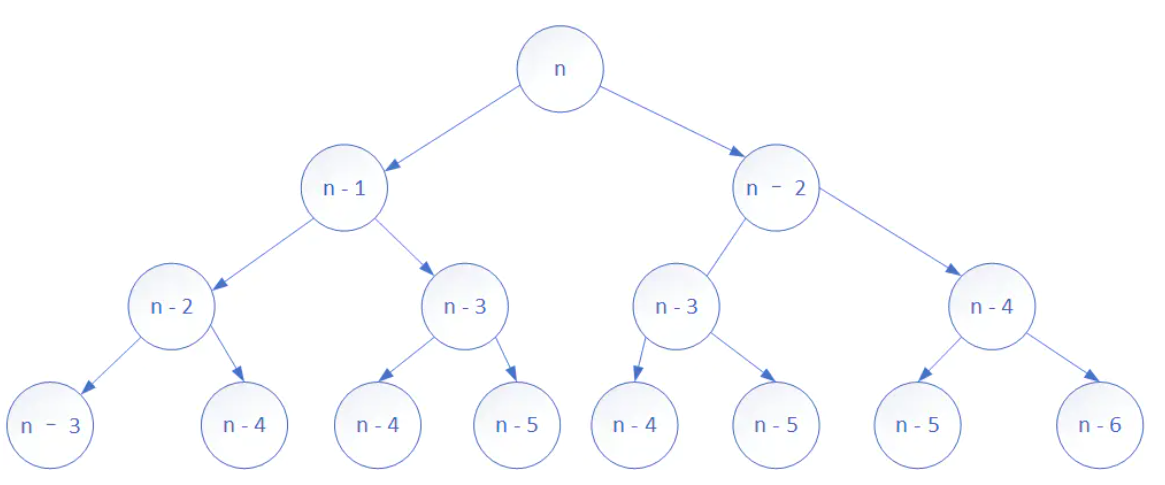
image.png

可以看到上面很多情况做了不止一次的计算，所以这里我们可以将每种情况的数据存入哈希表中，每次计算前先判断当前情况是否计算过，如果当前的情况有数据存在则不再重复计算并且返回该数据

class Solution:
    calculated = {}

    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        if n not in self.calculated:
            self.calculated[n] = self.climbStairs(n - 1) + self.climbStairs(n - 2)
            return self.calculated[n]
        return self.calculated[n]

这样每种情况只会被计算一遍，所以改良后的代码时间复杂度为 O(n)O(n)

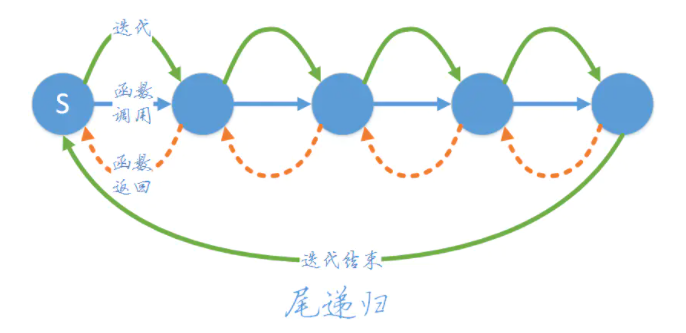
尾递归​

// 尾递归，进入下一个函数不再需要上一个函数的环境了，得出结果以后直接返回。
function story() {
    从前有座山，山上有座庙，庙里有个老和尚，一天老和尚对小和尚讲故事：story() 
}

即：尾递归函数的特点是在 回归过程中不用做任何操作，这个特性很重要，因为大多数现代的编译器会利用这种特点自动生成优化的代码。

那非尾递归是怎么样的？

// 非尾递归，下一个函数结束以后此函数还有后续，所以必须保存本身的环境以供处理返回值。
function story() {
    // 注意 “，小和尚听了，找了块豆腐撞死了” 需要等递归完成才能指向
    从前有座山，山上有座庙，庙里有个老和尚，一天老和尚对小和尚讲故事：story()，小和尚听了，找了块豆腐撞死了 
}

单向递归​

单向递归是指类似斐波那契数列那样往一个方向延展的递归

比如说兔子繁殖，一对兔子会繁殖一窝兔子，然后过几个月这些兔子长大了就会继续生小兔子，而且原来的兔子也会生出兔子 。。。。。。 之后兔子越来越多

单向递归 → 尾递归 → 迭代

递归转迭代​

理论上递归和迭代可以相互转换，但实际从算法结构来说，递归声明的结构并不总能转换为迭代结构（原因有待研究）。

所以迭代可以转换为递归，但递归不一定能转换为迭代。

将递归算法转换为非递归算法有两种方法，

  • 一种是直接求值（迭代），不需要回溯。它使用一些变量保存中间结果，称为直接转换法
  • 另一种是不能直接求值，需要回溯。它使用栈保存中间结果，称为间接转换法。

直接转换法​

直接转换法通常用来消除 尾递归（tail recursion）和 单向递归，将递归结构用迭代结构来替代。

间接转换法​

递归实际上利用了系统堆栈实现自身调用，我们通过使用栈保存中间结果模拟递归过程，将其转为非递归形式。

尾递归函数递归调用返回时正好是函数的结尾，因此递归调用时就不需要保留当前栈帧，可以直接将当前栈帧覆盖掉。

Reference​

参考资料 深入理解递归 参考资料 一文学会递归解题（超级棒！！）